GROUPES (mathématiques) - Groupes de Lie

GROUPES (mathématiques) - Groupes de Lie

La théorie des groupes de Lie, fondée dans la période de 1870-1880 par le mathématicien norvégien Sophus Lie, a d’abord été considérée comme une partie assez marginale des mathématiques, liée à des problèmes touchant les équations différentielles, les équations aux dérivées partielles et la géométrie différentielle. Leur étude générale a mis plus tard en évidence un certain nombre d’objets mathématiques particuliers, explicitement définis, les groupes semi-simples , dont on a peu à peu découvert le rôle fondamental dans presque toutes les parties des mathématiques modernes, même les plus éloignées en apparence des vues initiales de Lie. En outre, ces groupes semblent intervenir de façon de plus en plus profonde dans les conceptions récentes de la physique théorique, surtout en théorie de la relativité et en mécanique quantique.

On suppose connues les notions fondamentales relatives aux variétés différentielles et analytiques ^{[cf. VARIÉTÉS DIFFÉRENTIABLES]}. On utilisera systématiquement ici les notions introduites dans l’article sur les groupes classiques, qui constituent les premiers et les plus importants exemples de groupes de Lie.

1. La structure des groupes de Lie généraux

Un groupe de Lie (appelé aussi groupe de Lie réel ) est, par définition, une variété analytique réelle G (dite sous-jacente au groupe), munie d’une loi de composition (x , y) 料 xy pour laquelle G est un groupe, et qui est telle que l’application (x , y ) 料 xy ^-1 de G 憐 G dans G soit analytique. Une variété analytique complexe G munie d’une loi de composition (x , y ) 料 xy pour laquelle G est un groupe, et qui est telle que (x , y ) 料 xy ^-1 soit une application holomorphe de G 憐 G dans G, est appelée groupe de Lie complexe ; un tel groupe peut évidemment aussi être considéré comme groupe de Lie réel (dit sous-jacent au groupe de Lie complexe), en n’envisageant que sa structure de variété analytique réelle. Dans un groupe de Lie réel (resp. complexe) G, les translations x 料 ax , x 料 xa et les automorphismes intérieurs:

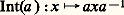sont des applications analytiques (resp. holomorphes); il en résulte que la dimension (resp. la dimension complexe) de la variété sous-jacente à G est la même en tous les points de G; on dit que c’est la dimension (resp. la dimension complexe ) de G; si G est un groupe de Lie complexe de dimension complexe n , le groupe de Lie réel sous-jacent est de dimension 2 n .

Un sous-groupe de Lie (resp. sous-groupe de Lie complexe ) H d’un groupe de Lie (resp. groupe de Lie complexe) G est un sous-groupe de G dont l’ensemble sous-jacent est une sous-variété fermée de la variété sous-jacente à G. On montre qu’un sous-groupe fermé d’un groupe de Lie G est nécessairement un sous-groupe de Lie de G (mais non nécessairement un sous-groupe de Lie complexe lorsque G est un groupe de Lie complexe).

Ainsi, le groupe linéaire GL (n , R) (resp. GL(n , C)) est un groupe de Lie réel (resp. complexe) de dimension (resp. de dimension complexe) n ²; le groupe unimodulaire SL(n , R) (resp. SL(n , C)) en est un sous-groupe de Lie (resp. un sous-groupe de Lie complexe) de dimension (resp. de dimension complexe) n ² 漣 1. Le groupe orthogonal O(n , R) (resp. O(n , C)) est un sous-groupe de Lie (resp. un sous-groupe de Lie complexe) de GL(n , R) (resp. GL(n , C) de dimension (resp. de dimension complexe) n (n 漣 1)/2.

Un homomorphisme f : GG de groupes de Lie (resp. de groupes de Lie complexes) est un homomorphisme de groupes qui est en même temps une application analytique (resp. holomorphe). Le noyau f ^-1(e ) est un sous-groupe de Lie (resp. un sous-groupe de Lie complexe) de G. Par contre, l’image f (G) est un sous-groupe de G qui n’est pas nécessairement fermé.

On se bornera, dans ce chapitre, aux propriétés des groupes de Lie réels; lorsqu’on mentionnera un groupe de Lie complexe, par exemple GL(n , C), c’est en fait le groupe de Lie réel sous-jacent dont il sera question.

Si N est un sous-groupe de Lie distingué d’un groupe de Lie G (donc fermé dans G), on peut définir sur le groupe G/N une structure et une seule de variété analytique qui en fait un groupe de Lie et pour laquelle l’application canonique:

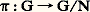est une submersion. Si G et G sont deux groupes de Lie, la structure de variété produit sur G 憐 G définit sur ce groupe une structure de groupe de Lie. Plus généralement, soit L et N deux groupes de Lie, et x 料 精^x un homomorphisme du groupe L dans le groupe Aut(N) des automorphismes de N, tel que l’application (x , y ) 料 精^x (y ) de L 憐 N dans N soit analytique. Alors le produit semi-direct L 憐 size=1^精 N de L par N relatif à 精 est un groupe de Lie pour la structure de variété produit; N est un sous-groupe distingué fermé de L 憐 size=1^精 N, et le groupe quotient:

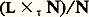est isomorphe à L.

Les groupes de Lie de dimension 0 sont les groupes discrets . Dans un groupe de Lie G, la composante neutre (c’est-à-dire la composante connexe de l’élément neutre e de G) est un sous-groupe ouvert (donc à plus forte raison fermé) distingué G⁰, et le quotient G/G⁰ est discret; on notera que G n’est pas nécessairement produit semi-direct de G⁰ et d’un sous-groupe isomorphe à G/G⁰. L’étude des groupes de Lie se concentre presque exclusivement sur les groupes de Lie connexes .

Pour un groupe de Lie connexe G, il existe un groupe de Lie simplement connexe G appelé revêtement universel de G, déterminé à un isomorphisme près, tel que G soit isomorphe à G/D, où D est un sous-groupe discret du centre de G, isomorphe au groupe fondamental 神¹(G) de la variété sous-jacente à G (le groupe 神¹(G) est donc toujours commutatif ). La structure des groupes de Lie connexes est donc ramenée à celle des groupes simplement connexes .

Ainsi le groupe GL(n , C) est connexe; mais le groupe GL(n , R) a deux composantes connexes, la composante neutre étant l’ensemble des matrices de déterminant strictement positif. Les groupes SL(n , C) et SL(n , R) sont connexes. Chacun des groupes O(n , C) et O(n , R) a deux composantes connexes; les composantes neutres sont SO(n , C) et SO(n , R).

Un groupe de Lie commutatif connexe est nécessairement isomorphe à un groupe du type R^p 憐 T^q , où T = R/Z («tore à une dimension»); son revêtement universel est R^p+q . Le groupe SL(n , C) est simplement connexe, mais GL(n , C) ne l’est pas: son revêtement universel est isomorphe à:

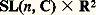et son groupe fondamental isomorphe à Z. Le groupe SO(2, R) est commutatif et isomorphe à T; pour n 閭 3, le groupe SO(n , R) a pour revêtement universel le groupe Spin(n ) (cf. GROUPES – Groupes classiques et géométrie) noté encore Spin(n , R), et le groupe fondamental est d’ordre 2; on définit de même le groupe Spin(n , C), qui est revêtement universel de SO(n , C) pour n 閭 3, avec encore un groupe fondamental d’ordre 2.

Dans un groupe de Lie simplement connexe G, les groupes dérivés successifs D^r (G) sont des sous-groupes distingués fermés connexes; il en est de même des sous-groupes C^r (G) de la série centrale descendante. Un groupe simplement connexe résoluble G a une variété sous-jacente isomorphe à un espace Rⁿ ; son groupe dérivé D(G) est nilpotent, et il existe une suite croissante (H^j ), 0 諒 j 諒 n , de sous-groupes fermés distingués de G telle que H⁰ =e, Hⁿ = G et que H^j+1 /H^j soit isomorphe à R. Par exemple, le groupe trigonal large supérieur T(n , R) formé des matrices réelles:

telles que x ^ij = 0, pour i 礪 j , est un groupe simplement connexe résoluble. Son groupe dérivé est le groupe trigonal strict supérieur , qui est formé des matrices de T(n , R) telles que x ⁱⁱ = 1 pour tout i . Tout groupe de Lie résoluble simplement connexe est isomorphe à un sous-groupe d’un groupe trigonal T(n , R). On notera qu’un groupe résoluble de dimension 閭 2 peut avoir son centre réduit à l’élément neutre, par exemple le groupe des matrices réelles:

où x 礪 0.

Dans un groupe de Lie connexe G, il existe un plus grand sous-groupe résoluble connexe R distingué dans G, appelé le radical de G; il est fermé dans G. Lorsque R est réduit à l’élément neutre, on dit que le groupe G est semi-simple . Pour un groupe de Lie connexe G, de radical R, S = G/R est semi-simple. Pour qu’un groupe connexe soit semi-simple, il faut et il suffit que son revêtement universel le soit. Un groupe de Lie simplement connexe G est produit semi-direct de son radical R et d’un groupe semi-simple L isomorphe à G/R. Le centre d’un groupe semi-simple est discret.

2. Groupes de Lie compacts et groupes semi-simples

Soit G un groupe de Lie connexe; il existe alors dans G un sous-groupe compact maximal K et un nombre fini de sous-groupes fermés H¹, ..., H^p isomorphes à R, tels que l’application: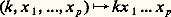

du produit:

soit un isomorphisme de la variété sous-jacente à ce produit sur la variété sous-jacente à G; en outre, pour tout sous-groupe compact K¹ de G, il existe s 捻 G tel que: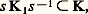

et en particulier deux sous-groupes compacts maximaux sont conjugués. Les propriétés topologiques de G (par exemple ses groupes d’homotopie ou d’homologie, cf. TOPOLO- GIE – Topologie algébrique) sont donc connues lorsqu’on connaît les propriétés correspondantes de K.

On peut citer deux exemples: dans SL(n , R), le groupe SO(n , R) est un sous-groupe compact maximal; dans GL(n , C), le groupe U(n , C), aussi noté U(n ), est un sous-groupe compact maximal.

Le revêtement universel d’un groupe de Lie compact K est de la forme K 憐 Rⁿ , où K est compact, semi-simple et simplement connexe. Tout groupe compact semi-simple et simplement connexe est produit direct de sous-groupes compacts simplement connexes et simples (c’est-à-dire n’ayant pas de sous-groupe fermé distingué distinct d’eux-mêmes et de dimension strictement positive); leurs centres sont finis, et les sous-groupes distingués fermés d’un groupe simple sont contenus dans le centre.

Les groupes simples compacts simplement connexes sont explicitement connus (classification de Killing-É. Cartan): il y a d’abord quatre séries infinies de groupes classiques (tabl. 1).

Les groupes de types B, C peuvent être définis pour m 閭 1 et ceux du type D pour m 閭 2, mais on n’obtient pas de groupes essentiellement nouveaux, car on a les isomorphismes A¹ 力 B¹ 力 C¹, B² 力 C² et A³ 力 D³, et le groupe de type D² est isomorphe au produit de deux groupes de type A¹. Il faut enfin préciser que le groupe unitaire U(m , H) sur le corps des quaternions H se rapporte à une forme unitaire positive non dégénérée.

Il existe en outre cinq groupes exceptionnels , notés:

(la seconde colonne indique la dimension, et la troisième, l’ordre du centre).

On verra plus loin (chap. 2, 3 et 4) d’autres précisions sur ces groupes. Mentionnons ici que l’algèbre de cohomologie des groupes classiques est entièrement déterminée sur l’anneau des entiers ou sur un corps premier; on connaît aussi les groupes d’homotopie:

pour k 諒 2 n + 2; en particulier:

pour k impair 麗 2 n ;

pour k pair 麗 2 n , et

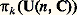
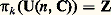
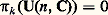
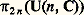est cyclique d’ordre n !; on obtient des résultats analogues pour les groupes d’homotopie de SO(n , R) (théorèmes de Bott).

Les groupes semi-simples complexes correspondent biunivoquement aux groupes semi-simples compacts , tout groupe semi-simple compact K étant sous-groupe compact maximal d’un groupe semi-simple complexe G, déterminé à isomorphie près, de dimension complexe égale à la dimension de K et dont le centre est celui de K (cf. chap. 6 et 7). Pour les groupes compacts classiques, les groupes simples complexes simplement connexes correspondants sont les suivants:

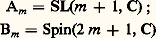(revêtement universel de SO(2 m + 1, C));

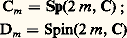(revêtement universel de SO(2 m , C).

La situation est plus compliquée pour les groupes semi-simples réels non compacts (et non sous-jacents à un groupe semi-simple complexe); ils peuvent avoir un centre infini (discret) et ne contenir aucun sous-groupe compact distinct dee (par exemple le revêtement universel de SL(2, R)). On se limitera ici aux groupes semi-simples réels dont le centre est fini (le quotient d’un groupe semi-simple par son centre, cf. chap. 5, a toujours un centre réduit à e ). Un tel groupe G^c de dimension n est sous-groupe fermé d’un groupe semi-simple complexe G^c , bien déterminé à isomorphie près (le «complexifié» de G, cf. chap. 7), de dimension complexe n ; mais à un même groupe semi-simple complexe G correspondent plusieurs groupes semi-simples réels non isomorphes, dont G est le complexifié; on dit que ces groupes sont les «formes réelles» de G ; une d’entre elles est toujours le groupe compact correspondant à G . Cependant, si, par exemple, on considère, pour un entier m 閭 2 donné et pour chaque p tel que 1 諒 p 諒 m , le groupe orthogonal réel unimodulaire:

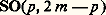correspondant à une forme quadratique de signature (p , 2 m 漣 p ), tous ces groupes sont des formes réelles, deux à deux non isomorphes, du groupe semi-simple complexe SO(2 m , C). Toutes les formes réelles des groupes simples complexes ont été déterminées par É. Cartan.

Un groupe semi-simple réel connexe non compact G admet toujours une décomposition d’Iwasawa G = KAN, où K est un groupe compact maximal de G, A un groupe commutatif fermé dans G, isomorphe à un Rⁿ , et N un groupe résoluble simplement connexe (donc ayant une variété sous-jacente isomorphe à un R^q ) fermé dans G; le centre de G est contenu dans KA; en outre, l’application:

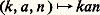est un isomorphisme de la variété sous-jacente à:

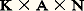sur la variété sous-jacente à G. Par exemple, si G = SL(n , R), on peut prendre pour K le groupe orthogonal SO(n , R), A est le groupe des matrices diagonales de déterminant 1, et N le groupe trigonal strict. Si:

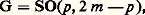on peut prendre pour K le produit:

Revenons aux groupes de Lie compacts . Un tel groupe K contient des sous-groupes compacts connexes commutatifs , donc isomorphes à des tores T^k . Un tore maximal T dans K est son propre centralisateur (donc contient le centre de K) et, pour tout autre tore T 說 K, il existe un s 捻 K tel que s T s ^-1 說 T; en particulier, deux tores maximaux sont toujours conjugués dans K. En outre, tout élément de K appartient à au moins un tore maximal. Ainsi, dans le groupe unitaire U(n , C), un groupe compact maximal est formé des matrices diagonales: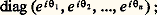

le fait que la réunion des tores maximaux est U(n , C) équivaut ici à la classique réduction d’une matrice unitaire à la forme diagonale par similitude.

La dimension m d’un tore maximal de K est appelée le rang de K; lorsque K est simple, le rang est l’indice m affixé à la lettre A, B..., G dans la classification de Killing-Cartan. Le normalisateur N(T) d’un tore maximal T d’un groupe semi-simple compact K joue un rôle important: le groupe quotient W = N(T)/T est appelé groupe de Weyl du groupe K (cf. chap. 6).

3. Actions des groupes de Lie

Les groupes de Lie ont d’abord été étudiés en tant que groupes de transformations de certains espaces, plutôt que pour eux-mêmes; et, dans la théorie moderne, les diverses façons dont un groupe de Lie peut être considéré comme groupe de transformations jouent encore un grand rôle. Les actions ou opérations d’un groupe de Lie se définissent comme pour les groupes quelconques (cf. GROUPES – Représentation linéaire des groupes), mais on n’envisage d’ordinaire que des actions d’un groupe de Lie G sur une variété analytique X, et on exige que l’application (s, x ) 料 s . x de G 憐 X dans X soit analytique. Pour tout s 捻 G, l’application x 料 s . x est alors un isomorphisme de la variété X sur elle-même; pour tout x 捻 X, l’ensemble S^x des s 捻 G tels que s . x = x est un sous-groupe fermé de G appelé stabilisateur de x . L’ orbite G . x de x est l’ensemble des s . x pour s 捻 G; les orbites sont les classes d’équivalence d’une relation d’équivalence R dans G; elles ne sont pas nécessairement fermées dans X et peuvent être en fait des ensembles très compliqués. Leur étude générale n’a guère été poussée que pour G = R ou G = Z (cf. théorie ERGODIQUE).

L’ensemble X/G des orbites ne peut en général être muni d’une structure de variété analytique telle que l’application canonique 神: XX/G (qui fait correspondre à un point son orbite) soit une submersion; pour qu’il en soit ainsi, il faut et il suffit que l’ensemble 臨^R 說 X 憐 X des couples (x , y ) appartenant à une même orbite soit une sous-variété fermée de X 憐 X; toute orbite est alors une sous-variété fermée de X.

Un cas où la variété des orbites existe toujours est celui où G est un sous-groupe fermé d’un groupe de Lie H, le groupe G opérant dans H par translation à droite (s , x ) 料 xs avec s 捻 G, x 捻 H, de sorte que les orbites sont les classes à gauche x G dans H. La variété des orbites H/G est alors appelée l’espace homogène des classes à gauche suivant G; le groupe de Lie H opère à gauche sur H/G par (z , x G) 料 zx G. Lorsqu’un groupe de Lie G opère sur une variété X de sorte que la variété des orbites X/G soit définie, l’orbite d’un point x est canoniquement isomorphe à l’espace homogène G/S^x .

Le fait pour une variété analytique de X de pouvoir être considérée comme espace homogène H/G d’un groupe de Lie H implique l’existence sur X d’une «géométrie» où se reflètent les propriétés des groupes H et G: c’est l’idée directrice exprimée d’abord par F. Klein dans son programme d’Erlangen, et la géométrie euclidienne classique n’apparaît plus ainsi que comme un exemple particulier des «géométries» associées aux groupes de Lie; les plus intéressantes correspondent au cas où H est un groupe simple (cf. chap. 2) et on a par exemple développé ainsi les «géométries de Tits-Freudenthal» correspondant aux cinq groupes exceptionnels.

Les espaces homogènes G/H les plus importants dans toutes sortes d’applications sont les espaces riemanniens symétriques irréductibles , découverts et entièrement énumérés par É. Cartan au cours de recherches de géométrie riemannienne: ce sont les espaces de la forme G/K, où G est un groupe simple réel de centre fini et K un sous-groupe compact de G, obtenu comme l’ensemble des x 捻 G tels que 靖(x ) = x où 靖 est une involution analytique de G (cf. chap. 7). Lorsque G est non compact, K est nécessairement un sous-groupe compact maximal de G, et G/K est difféomorphe à un espace Rⁿ . Si l’on prend G = SL(n , R), par exemple, K = SO(n , R) est l’ensemble des matrices invariantes par l’involution U 料 靖(U ) = ^t U ^-1 (contragédiente de U ); pour n = 2, l’espace symétrique G/K s’identifie canoniquement avec le demi-plan de Poincaré formé des nombres complexes de parties imaginaires strictement positives, où la matrice:

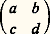de G opère par:

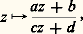avec a , b , c , d réels et ad 漣 bc = 1. Dans beaucoup de cas (entièrement déterminés par É. Cartan), les espaces symétriques G/K s’identifient ainsi à des ouverts d’espaces complexes Cⁿ , où G opère par transformations holomorphes , et ces espaces jouent un rôle important dans la théorie des fonctions de plusieurs variables complexes (cf. FONCTIONS ANALYTIQUES – Fonctions analytiques de plusieurs variables complexes). Plus récemment, on a pu déterminer également les ouverts bornés de Cⁿ qui sont des espaces homogènes G/H (non nécessairement symétriques) où G opère par transformations holomorphes. Les sphères et les espaces projectifs sont aussi des espaces riemanniens symétriques irréductibles.

4. Représentations linéaires de dimension finie des groupes de Lie

Les définitions sont données à l’article précédent, qui traite de la représentation linéaire des groupes ; on se bornera aux représentations linéaires dans des espaces vectoriels V (de dimension finie dans ce chapitre) sur le corps C des nombres complexes ; en outre, les représentations linéaires 福: GGL(V) d’un groupe de Lie que l’on considère sont supposées analytiques (réelles).

Lorsque le groupe de Lie G est connexe et résoluble , toute représentation irréductible de G est de dimension 1, autrement dit de la forme s 料 﨑(s ), où 﨑 est un caractère (abélien) du groupe commutatif G/D(G); une représentation quelconque de G s’écrit toujours sous la forme triangulaire:

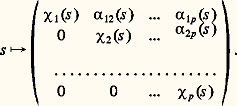L’exemple de la représentation linéaire:

de G = R montre qu’une représentation linéaire d’un groupe commutatif n’est pas nécessairement complètement réductible.

En revanche, toute représentation linéaire d’un groupe de Lie G compact ou réductif (c’est-à-dire dont le revêtement universel est produit d’un groupe semi-simple et d’un Rⁿ ) est complètement réductible (théorème de H. Weyl); pour les groupes compacts, c’est même vrai sans supposer que G est un groupe de Lie (cf. art. précédent). Tout revient donc à déterminer, dans ces cas, les représentations irréductibles ; cette détermination a été complètement effectuée par É. Cartan au moyen de techniques qui seront esquissées dans le chapitre 6.

La théorie des représentations linéaires des groupes semi-simples généralise la théorie classique des invariants en géométrie projective. Il s’agissait uniquement, dans cette théorie, des représentations des groupes classiques, et surtout de SL(V). Ce groupe opère en effet naturellement dans toute puissance tensorielle V size=1^辰n , et dans le sous-espace des tenseurs symétriques d’ordre n. Ce dernier s’identifie à l’espace vectoriel Fⁿ des polynômes homogènes de degré n à p variables (si p = dim V); un élément s 捻 SL(V) opère en transformant un tel polynôme Pⁿ (x ¹, ..., x ^p ) en le polynôme: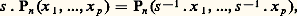

en posant s ^-1 . x ^k = a ^k1 x ¹ + ... + a ^kp x ^p si s ^-1 est la matrice (a ^ij ). Un invariant dans Fⁿ est un polynôme tel que s . Pⁿ = Pⁿ pour tout s 捻 SL(V); cela signifie que Pⁿ engendre dans Fⁿ un sous-espace stable de dimension 1, et, si l’on sait décomposer toute représentation linéaire en représentations irréductibles, on pourra obtenir tous les invariants. D. Hilbert avait démontré (pour SL(V)) qu’il y a un nombre fini de polynômes homogènes invariants I¹, I², ..., I^r tel que tout autre invariant soit de la forme Q(I¹, I², ..., I^r ), où Q est un polynôme. Ce théorème s’étend à tous les groupes semi-simples (mais non à tous les groupes de Lie).

Une représentation linéaire:

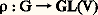est dite fidèle si elle est injective. On peut prouver que, pour tout groupe de Lie connexe G, il existe un groupe connexe qui a même revêtement universel que G et qui est isomorphe à un sous-groupe d’un groupe linéaire GL(V); mais le revêtement universel de G n’a pas toujours cette propriété (par exemple pour G = SL(2, R)). Toutefois, tout groupe compact et tout groupe semi-simple complexe est isomorphe à un sous-groupe d’un groupe linéaire.

5. Algèbres de Lie

L’outil essentiel dans la démonstration des remarquables résultats qui précèdent est la méthode infinitésimale, inaugurée par S. Lie (1842-1899), qui a pour effet de ramener l’étude des groupes de Lie à l’étude de ce qu’on appelle leurs algèbres de Lie. L’idée est d’étudier les conditions qu’impose l’associativité de la loi d’un groupe G aux séries qui l’expriment dans un voisinage V de e. On suppose choisi un système de coordonnées locales qui s’annulent en e , de sorte que V est identifié à un voisinage de l’origine dans Rⁿ . Soit W un voisinage de 0 tel que W² 說 V, et x = (x ¹, ..., x ⁿ ), y = (y ¹, ..., y ⁿ ) deux points de W; leur produit z = xy 捻 V étant fonction analytique de x , y par hypothèse, les coordonnées z ¹, ..., z ⁿ de z s’expriment par des séries convergentes pour |x ^j | 麗 福, |y ^j | 麗 福, 1 諒 j 諒 n :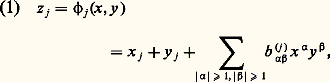

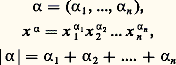1 諒 j 諒 n , où l’on a employé la notion des multi-indices:

(cf. CALCUL INFINITÉSIMAL – Calcul à plusieurs variables). Considérons alors une fonction analytique:

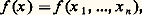donc développable en série convergente au voisinage de 0; si l’on substitue à chaque x ^j la série z ^j = 﨏^j (x , y ) donnée par (1), on obtient une série en les x ^j et y ^j , et, en groupant les monômes en x size=1^廓y size=1^見 pour un même 見, on obtient ce qu’on peut appeler la formule de Taylor dans le groupe G au voisinage de e :

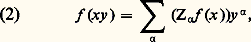où on vérifie aisément que:

(combinaison d’un nombre fini de dérivées partielles de f , à coefficients a size=1^見廓 analytiques au voisinage de 0). Les applications f 料 Z size=1^見f sont donc des opérateurs différentiels sur les fonctions analytiques dans G; en outre, ils ont la propriété fondamentale d’invariance à gauche par le groupe. De façon précise, pour tous s 捻 G assez petit, posons f ^s (x ) = f (sx ). Un opérateur différentiel Z est dit invariant à gauche si Z(f ^s ) = (Z(f ))^s , pour s assez petit; pour les Z size=1^見, cela résulte de leur définition (2) et de l’associativité, qui donne f ^s (xy ) = f ((sx )y ). Il est clair que l’ensemble face=F9828 G des opérateurs différentiels invariants à gauche est une algèbre associative sur R, dont on voit aisément que les Z size=1^見 forment une base sur R (Z⁰ est pris égal à l’identité). En fait, la table de multiplication de la base (Z size=1^見) se détermine explicitement à l’aide des séries (1). On pose en effet, pour tout multi-indice 塚 = ( 塚¹, ..., 塚ⁿ ):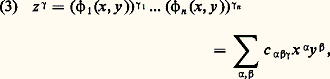

de sorte que b ^{(j )} size=1^見廓 = c size=1^見廓﨎j , où 﨎^j est le multi-indice ( 嗀^ij ), avec 1 諒 i 諒 n ; de plus, on vérifie aussitôt que c size=1^見廓塚 = 0 pour | 見| + | 廓| 麗 | 塚| et que les seuls c size=1^見廓塚 non nuls tels que | 塚| = | 見| + | 廓| sont ceux pour lesquels 塚 = 見 + 廓, qui ont pour valeur:

avec 見! = 見¹! ... 見ⁿ !. Pour tout s assez petit, on peut écrire:

et, en vertu de la formule (2) appliquée en remplaçant f par Z size=1^廓f :

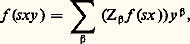
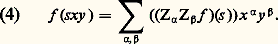Mais, d’autre part, on a aussi, par (2):

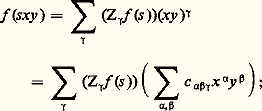d’où, en comparant à (4), les formules:

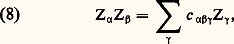qui donnent la table de multiplication. La comparaison des formules (3) et (5) montre que la structure d’algèbre de face=F9828 G et la structure de groupe de G (si G est simplement connexe) se déterminent mutuellement sans ambiguïté.

En particulier, en posant:

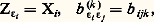on tire de (5), en prenant 見 = 﨎ⁱ , 廓 = 﨎^j :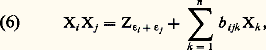

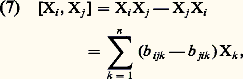1 諒 i 諒 n et 1 諒 j 諒 n ; et, en échangeant i et j :

1 諒 i 諒 n et 1 諒 j 諒 n .

Le sous-espace vectoriel face=F9828 g de face=F9828 G, de dimension n , admettant les Xⁱ pour base, est l’ensemble des opérateurs invariants à gauche d’ordre 1; les formules (7) montrent que face=F9828 g est stable pour l’opération:

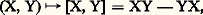qui vérifie les deux identités:

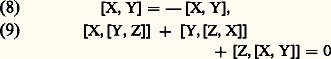(identité de Jacobi). Un espace vectoriel sur un corps K dans lequel est défini une loi de composition:

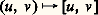vérifiant ces deux identités et bilinéaire est appelé algèbre de Lie sur K. Un homomorphisme f : face=F9828 gface=F9828 g d’algèbres de Lie sur le même corps est par définition une application K-linéaire telle que:

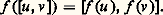On a donc associé canoniquement à tout groupe de Lie G une algèbre de Lie face=F9828 g sur R, dite algèbre de Lie de ce groupe et notée Lie (G). Il est très facile, en partant des formules (4) et (5) et des propriétés des c size=1^見廓塚, de voir que les Xⁱ engendrent l’algèbre associative face=F9828 G; de façon précise, les monômes:

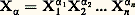forment une base de l’espace vectoriel face=F9828 G (l’ordre des facteurs dans les X size=1^見 est bien entendu essentiel). De plus face=F9828 G est entièrement déterminée à isomorphie près lorsqu’on connaît face=F9828 g, car elle est caractérisée par la propriété «universelle» suivante: Pour toute application linéaire f de face=F9828 g dans une R-algèbre associative A telle que:

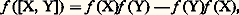il existe un homomorphisme d’algèbres F de face=F9828 G dans A et un seul qui prolonge f .

Lorsque G est un groupe de Lie complexe, son algèbre de Lie face=F9828 g est une algèbre de Lie sur le corps C; quand on la considère comme algèbre de Lie sur R, elle est l’algèbre de Lie du groupe réel sous-jacent à G.

Voici quelques exemples. Si G = Rⁿ , on a:

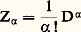et (2) est la formule de Taylor usuelle; l’algèbre associative face=F9828 G s’identifie à l’algèbre des polynômes en les D^j , 1 諒 j 諒 n ; l’algèbre de Lie correspondante est commutative , c’est-à-dire que [X, Y] = 0 quels que soient X, Y dans face=F9828 g. L’algèbre de Lie du groupe des matrices:

a une base de deux éléments X, Y vérifiant la table de multiplication [X, Y] = 漣 Y. L’algèbre de Lie face=F9828 gl(n , R) (resp. face=F9828 gl(n , C)) du groupe linéaire GL(n , R) (resp. GL(n , C)) s’identifie canoniquement à l’espace des matrices carrées réelles (resp. complexes) d’ordre n où le crochet est l’application (X , Y ) 料 XY 漣 YX ; l’algèbre de Lie de SL(n , R) est la sous-algèbre de Lie face=F9828 sl(n , R) de face=F9828 gl(n , R) formée des matrices de trace 0. En particulier, face=F9828 sl(2, R) (ou face=F9828 sl(2, C)) a pour base les trois matrices:

vérifiant donc la table de multiplication: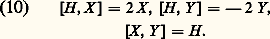

On montre que réciproquement, à toute algèbre de Lie face=F9828 g sur R (resp. C) de dimension finie, correspond un groupe de Lie réel (resp. complexe) simplement connexe et un seul à isomorphie près, dont l’algèbre de Lie est isomorphe à face=F9828 g. Tous les groupes de Lie connexes ayant la même algèbre de Lie ont même revêtement universel (à isomorphie près). Cette correspondance permet d’établir un «dictionnaire» entre les notions fondamentales de la théorie des groupes de Lie et des notions de la théorie des algèbres de Lie, qui relèvent essentiellement de l’algèbre linéaire (pour deux sous-espaces vectoriels face=F9828 a, face=F9828 b d’une algèbre de Lie face=F9828 g, on note dans ce qui suit [ face=F9828 a, face=F9828 b] le sous-espace vectoriel engendré par les [X, Y] pour X 捻 face=F9828 a, Y 捻 face=F9828 b) selon le tableau 2.

Pour tout s 捻 G, il correspond à l’automorphisme intérieur Int(s ): x 料 sxs ^-1 de G l’automorphisme dérivé (Int(s )) de face=F9828 g, noté Ad(s ); l’application s 料 Ad(s ) de G dans GL(face=F9828 g) est une représentation linéaire de G dans l’espace vectoriel face=F9828 g, appelée représentation adjointe ; son noyau est le centre Z de G et son image Ad(G) 說 GL(face=F9828 g), isomorphe à G/Z, est appelée le groupe adjoint de G. On montre que la représentation linéaire Ad de face=F9828 g dans face=F9828 gl(face=F9828 g) est l’application X 料 ad(X), où on pose:

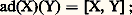cette application est dite représentation adjointe de face=F9828 g; son noyau est le centre face=F9828 z de face=F9828 g et, pour tout X 捻 face=F9828 g, ad(X) est une dérivation de l’algèbre face=F9828 g, c’est-à-dire:

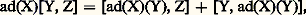ce qui n’est autre que l’identité de Jacobi.

Pour tout X 捻 face=F9828 g, il existe un homomorphisme et un seul du groupe additif R dans G, dont l’homomorphisme dérivé soit t 料 t X; on note cet homomorphisme t 料 exp(t X) et l’image de R par cet homomorphisme est appelée le sous-groupe à un paramètre de G correspondant à X. Un tel sous-groupe n’est pas nécessairement fermé dans G; ainsi, par exemple, si G = T² et si 﨏 : R 料 T est l’homomorphisme canonique, alors t 料 ( 﨏(t ), 﨏( t )), où est un nombre irrationnel, définit un sous-groupe à un paramètre partout dense dans T². On a:

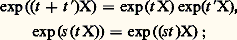par contre, si X et Y sont tels que [X, Y] 0, on a en général:

On montre qu’il existe un voisinage assez petit V de 0 dans face=F9828 g tel que l’application exponentielle X 料 exp(X) de face=F9828 g dans G, restreinte à V, soit un isomorphisme analytique de V sur un voisinage ouvert de e ; mais en général, l’application X 料 exp(X) n’est ni injective ni surjective dans face=F9828 g. Elle est toutefois surjective lorsque G est compact, et bijective lorsque G est résoluble et simplement connexe. On prouve, en outre, que: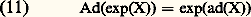

pour X 捻 g, l’exponentielle du second membre étant la série usuelle:

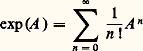dans l’algèbre des matrices.

6. Algèbres de Lie semi-simples

La notion d’algèbre de Lie résoluble (resp. nilpotente ) se définit comme pour les groupes, en remplaçant les groupes D^r (G) (resp. C^r (G)) par les idéaux formés de la façon correspondante dans l’algèbre de Lie face=F9828 g. Si G est un groupe de Lie simplement connexe, R son radical, le plus grand idéal résoluble face=F9828 r de l’algèbre de Lie face=F9828 g de G est l’algèbre de Lie de R, et on l’appelle le radical de face=F9828 g. Une algèbre de Lie face=F9828 g est dite semi-simple si son radical est réduit à0 (ou, ce qui revient au même, si elle ne contient pas d’idéal commutatif non réduit à0. Un groupe de Lie connexe est semi-simple si et seulement si son algèbre de Lie est semi-simple.

On définit d’autre part sur toute algèbre de Lie réelle (resp. complexe) face=F9828 g une forme bilinéaire symétrique réelle (resp. complexe) dite forme de Killing , par la formule :

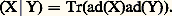Cette forme est étroitement liée à la structure de face=F9828 g par les trois critères de Cartan :

– Pour que face=F9828 g soit résoluble, il faut et il suffit que (X|Y) = 0 pour X 捻 face=F9828 g et Y 捻 [ face=F9828 g, face=F9828 g].

– Pour que face=F9828 g soit semi-simple, il faut et il suffit que la forme de Killing soit non dégénérée.

– Pour qu’une algèbre de Lie réelle face=F9828 g soit l’algèbre de Lie d’un groupe compact, il faut et il suffit que (X|X) 諒 0 dans face=F9828 g.

On peut parvenir à la détermination de la structure d’un groupe compact semi-simple G, en analysant sa représentation adjointe. Il est commode de commencer par étendre canoniquement chaque endomorphisme Ad(s ) (pour s 捻 G) de l’algèbre de Lie face=F9828 g à un endomorphisme de sa complexifiée face=F9828 g^c = face=F9828 g 辰R C, de sorte qu’on peut considérer G comme opérant par s 料 Ad(s ) soit sur face=F9828 g, soit sur face=F9828 g^c. L’idée fondamentale est de restreindre la représentation adjointe à un tore maximal T de G; comme T est compact et commutatif et que la forme de Killing est invariante par tout automorphisme de face=F9828 g et négative non dégénérée, cette représentation est complètement réductible, donc face=F9828 g se décompose en somme directe de sous-espaces E^k , deux à deux orthogonaux pour (X|Y), de dimension 1 ou 2 sur R, et stables par Ad(s ), s 捻 T; mais le cas dim(E^k ) = 1 est à exclure, car le groupe à un paramètre engendré par un élément de E^k commuterait alors avec T, contrairement à l’hypothèse que T est maximal. Alors:

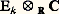est somme directe de deux sous-espaces E ^k et E ^k de dimension 1 sur C, dans lesquels on a:

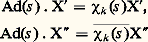respectivement, où 﨑^k est un caractère de T; en vertu de (11), il revient au même de dire que, pour tout

face=F9828 t = Lie(T), on a: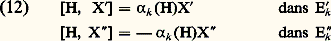

avec 﨑^k (exp(H)) = exp 2 神i 見^k (H), où 見^k est une forme linéaire non identiquement nulle sur face=F9828 h, à valeurs réelles dans face=F9828 t; on dit que les 見^k sont les racines de face=F9828 gc relativement à la sous-algèbre commutative maximale face=F9828 h. L’identité de Jacobi et le fait que face=F9828 h est maximale montrent que [E ^k , E ^k ] 說 face=F9828 h; on constate alors que la somme directe:

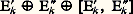est une sous-algèbre de face=F9828 g^c avec une base vérifiant (10), elle est donc isomorphe à face=F9828 sl(2,C). Une analyse élémentaire des représentations irréductibles de face=F9828 sl(2, C) permet d’obtenir les résultats fondamentaux suivants: toutes les racines 見^k (1 諒 k 諒 (n 漣 m )/2 si n = dim G, m = dim T) sont distinctes; on peut donc prendre leur ensemble R comme ensemble d’indices, écrire face=F9828 g size=1^見 et face=F9828 g^- size=1^見 au lieu de E ^k et E ^k , et déterminer dans chaque face=F9828 g size=1^見 un élément X size=1^見, de sorte que, si l’on pose:

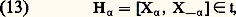on obtienne:

En outre, pour deux racines quelconques 見, 廓, le nombre 廓(H size=1^見) est égal à p 漣 q , où p et q sont deux entiers positifs ou nuls tels que les entiers k vérifiant 漣 p 諒 k 諒 q soient exactement ceux pour lesquels 廓 + k 見 est une racine (on montre qu’on a toujours p + q 諒 3); enfin: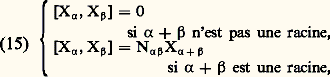

et l’on peut montrer que:

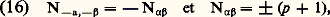où l’entier p a été défini ci-dessus (base de Weyl-Chevalley); les H size=1^見 engendrent face=F9828 t et l’on obtient:

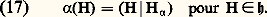On prouve, à l’aide de ces relations, que l’application:

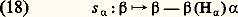est une permutation involutive de l’ensemble R des racines; de plus, si 見 捻 R, on a 2 見 殮 R. La détermination complète des ensembles finis R contenus dans le dual face=F9828 h de l’espace vectoriel face=F9828 h, ne contenant pas 0, engendrant face=F9828 h et ayant les deux propriétés précédentes (ensembles dénommés systèmes de racines ) est essentiellement un problème de géométrie élémentaire, qui conduit à la classification de Killing-Cartan (cf. chap. 2).

Ainsi, pour le type A^m , qui correspond à l’algèbre de Lie:

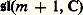du groupe unimodulaire, on peut prendre pour face=F9828 h l’algèbre de Lie engendrée par les éléments E ⁱⁱ 漣 E ^jj (E ^hk est la matrice ayant un seul élément 0, situé dans la h -ième ligne et la k -ième colonne, et égal à 1); les racines 見^ij correspondent aux couples (i , j ) tels que i j , avec 見^ji = 漣 見^ij ; on a: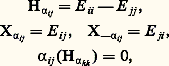

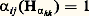si ni h ni k ne sont égaux à l’un des indices i , j , et

si h = i et j k , ou h i et j = k . On peut vérifier sur cet exemple les formules générales données plus haut.

Les racines 見 appartiennent en fait au dual face=F9828 t de l’espace vectoriel réel face=F9828 t; si on définit sur face=F9828 t la forme bilinéaire inverse de (U|V) sur face=F9828 t, qu’on note ( 﨡| 兀), la permutation s size=1^見 est la restriction à R de la réflexion orthogonale par rapport à l’hyperplan M size=1^見 des 﨡 捻 face=F9828 t tels que 﨡(H size=1^見) = 0. Les s size=1^見 pour 見 捻 R engendrent un groupe fini de transformations orthogonales, canoniquement isomorphe au groupe de Weyl W de G (cf. chap. 2) auquel on l’identifie. Les composantes connexes, dans l’espace face=F9828 t, de la réunion des hyperplans M size=1^見 sont appelées les chambres de face=F9828 g (relatives à face=F9828 t); pour une chambre C, il y a exactement m hyperplans M size=1^見 tels que la réunion des M size=1^見 惡 綠 constitue la frontière de 綠 (donc 綠 est un «angle polyèdre» dans l’espace face=F9828 t à m dimensions); on dit que ces hyperplans M size=1^見 sont les murs de C. Si on choisit une chambre C, et qu’on note Mⁱ (1 諒 i 諒 m ) ses murs, pour chaque i une des deux racines opposées orthogonales à Mⁱ est du même côté que C de Mⁱ ; elle est notée 見ⁱ et on dit que les 見ⁱ (qui forment une base de l’espace vectoriel face=F9828 t) forment une base du système de racines R. On prouve que toute racine 見 捻 R est combinaison linéaire des 見ⁱ à coefficients entiers de même signe ; les racines de R sont ainsi divisées en deux classes, dites positives (resp. négatives ) pour C si tous les coefficients sont 閭 0 (resp. 諒 0). Le groupe de Weyl permute les chambres (donc aussi les bases de R) de façon simplement transitive . Donnons un exemple: pour le type A^m , on peut prendre comme base les racines 見ⁱ ,ⁱ⁺¹ pour 1 諒 i 諒 m ; donc le groupe de Weyl s’identifie au groupe symétrique ^m+1 des permutations de m + 1 objets.

Supposons G simplement connexe. On a vu que les représentations linéaires de G dans un espace vectoriel complexe V correspondent biunivoquement aux représentations linéaires de face=F9828 g dans V, et aussi (puisque V est un espace vectoriel complexe) à celles de face=F9828 g^c dans V; ces dernières sont donc complètement réductibles, et il suffit de déterminer les représentations irréductibles de face=F9828 g^c. On utilise la même idée que ci-dessus, savoir la restriction à face=F9828 h d’une représentation 福 de face=F9828 g^c dans V; on appelle poids de la représentation 福 (irréductible ou non) tout élément 諸 捻 face=F9828 h pour lequel il existe un vecteur x 捻 V non nul et pour lequel:

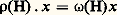pour tout H 捻 face=F9828 h (donc x est vecteur propre commun à tous les endomorphismes 福(H)); l’ensemble V size=1^諸 des vecteurs x ayant cette propriété pour un poids 諸 est un sous-espace vectoriel V size=1^諸 et V est somme directe des V size=1^諸. Les poids de 福 sont donc en nombre fini; si l’on suppose maintenant 福 irréductible et si l’on choisit une base ( 見ⁱ ) de R, avec 1 諒 i 諒 m , on démontre qu’il existe un unique poids 神 de 福 tel que tous les autres poids de 福 soient de la forme:

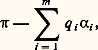où les q ⁱ sont des entiers positifs ; on dit que 神 est le poids dominant de la représentation 福, et on montre que V size=1^神 est de dimension 1. Deux représentations irréductibles de face=F9828 g^c ayant même poids dominant sont semblables. Pour qu’une forme linéaire 諸 捻 face=F9828 h soit poids dominant d’une représentation irréductible de face=F9828 g^c, il faut et il suffit que l’on ait 諸(H size=1^見i ) 閭 0 pour 1 諒 i 諒 m . Les poids dominants de toutes les représentations irréductibles de face=F9828 g^c forment donc un Z-module libre P(R), ayant pour base les poids 神ⁱ (1 諒 i 諒 m ) tels que:

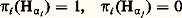pour i j ; les 神ⁱ sont appelés les poids fondamentaux de face=F9828 g^c (pour la base ( 見ⁱ )); on a évidemment R 說 P(R) et le sous-groupe Q(R) engendré par R est d’indice fini dans P(R); on prouve que le quotient P(R)/Q(R) est isomorphe au centre de G (supposé simplement connexe).

Ainsi, pour le type A^m , les poids fondamentaux 諸ⁱ (1 諒 i 諒 m ) sont donnés par :

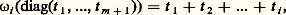qui est une fonction restreinte à la sous-algèbre face=F9828 h des matrices diagonales telles que:

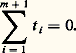On vérifie que 諸¹, est le poids dominant de la représentation identique:

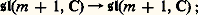on montre que 諸^j est le poids dominant de la représentation canonique dans la puissance extérieure j-ième de C^m+1 .

Le caractère (cf. art. précédent) de la représentation irréductible du groupe compact semi-simple G de poids dominant 諸 est donné par la formule de H. Weyl :

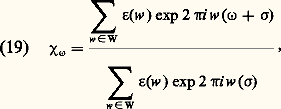où 靖 est la demi-somme des racines positives, w parcourt le groupe de Weyl et 﨎(w ) est son déterminant (égal à 梁 1 suivant que w est produit d’un nombre pair ou impair de réflexions s size=1^見); le caractère apparaît comme une fonction définie dans l’algèbre de Lie face=F9828 t de T, mais a la même valeur pour tous les éléments H 捻 face=F9828 t tels que exp(H) 捻 T ait la même valeur dans T (cela résulte de ce que 靖 est la somme des poids fondamentaux 諸ⁱ ); en fait, 﨑 size=1^諸 est donc définie dans T, et, comme tout élément de G est contenu dans un conjugué de T, 﨑 size=1^諸 est bien définie dans G.

En particulier, la dimension de l’espace de la représentation irréductible de poids dominant 諸 s’obtient en prenant la valeur de 﨑 size=1^諸 (H) pour H = 0, et on montre que cette valeur est:

(produit étendu aux racines positives).

7. Algèbres semi-simples complexes et leurs formes réelles

Dans le chapitre 6, en partant de l’algèbre de Lie d’un groupe semi-simple compact, on a obtenu, en la complexifiant, une algèbre de Lie semi-simple complexe. Ce processus admet une réciproque, qui établit une correspondance biunivoque entre groupes connexes semi-simples complexes et groupes connexes semi-simples compacts .

L’unique méthode connue pour établir ce fait est due à Killing et É. Cartan, et est fort longue: on commence par démontrer, dans une algèbre semi-simple complexe face=F9828 g de dimension n sur C, l’existence d’une sous-algèbre commutative maximale face=F9828 h (sous-algèbre de Cartan ) telle que la relation ad(X)(face=F9828 h) 說 face=F9828 h entraîne X 捻 face=F9828 h. En étudiant la représentation adjointe H 料 ad(H) de face=F9828 h dans l’espace vectoriel face=F9828 g, on arrive alors à décomposer face=F9828 g en somme directe de face=F9828 h et de sous-espaces CX size=1^見 de dimension 1, où les X size=1^見 vérifient les relations (13) à (16). On voit aisément que l’espace vectoriel réel face=F9828 u engendré par les i H size=1^見, les X size=1^見 漣 X size=1^漣 size=1^見 et les i (X size=1^見 + X size=1^漣 size=1^見) est une algèbre de Lie réelle dans laquelle la forme de Killing est négative non dégénérée; donc face=F9828 u est l’algèbre de Lie d’un groupe compact semi-simple U, et face=F9828 g = face=F9828 u 簾 i face=F9828 u. Les i H size=1^見 engendrent une sous-algèbre (réelle) commutative maximale face=F9828 t de face=F9828 u (correspondant à un tore maximal T de U), et on a face=F9828 h = face=F9828 t 簾 i face=F9828 t.

Si l’on choisit une base ( 見^j ), avec 1 諒 j 諒 m , du système des racines de face=F9828 g, la sous-algèbre (complexe) face=F9828 n⁺ (resp. face=F9828 n^-) de face=F9828 g ayant pour base les X size=1^見 pour 見 礪 0 (resp. 見 麗 0) est une sous-algèbre nilpotente ; on a: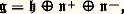

et face=F9828 b = face=F9828 h 簾 face=F9828 n⁺ est une sous-algèbre résoluble maximale de face=F9828 g. Si G est un groupe de Lie (complexe) connexe d’algèbre de Lie face=F9828 g et B le sous-groupe connexe de G correspondant à face=F9828 b, B est donc un sous-groupe résoluble connexe maximal de G. Les sous-groupes ayant ces trois propriétés sont appelés sous-groupes de Borel de G; ils sont tous conjugués dans G. On montre que B est son propre normalisateur dans G, et que l’espace homogène G/B est compact et peut canoniquement être muni d’une structure de variété algébrique projective sur C. En outre, les doubles classes Bs B forment une partition de G qui est canoniquement indexée par le groupe de Weyl W de U (décomposition de Bruhat ): de façon précise, pour tout w 捻 W, il existe, dans le normalisateur de T dans U, un élément n ^w tel que Ad(n ^w ) laisse stable face=F9828 h et induise sur face=F9828 h la contragrédiente de w considéré comme opérant dans face=F9828 h (cf. chap. 6); l’application w 料 Bn ^w B est une bijection de W sur l’ensemble des doubles classes modulo B.

Dans SL(n , C), par exemple, un groupe de Borel est le groupe trigonal large supérieur T(n , C) (cf. chap. 1).

Le groupe de Borel permet de donner une expression explicite de la représentation linéaire de G correspondant à une représentation linéaire de face=F9828 g de poids dominant 諸. Supposons, pour simplifier, G simplement connexe, et soit M le sous-groupe connexe de G correspondant à face=F9828 h, qui est isomorphe à (C)^m («groupe de type multiplicatif»); on déduit de 諸 un homomorphisme 祥 size=1^諸 : MC défini par:

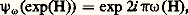coïncidant dans T avec le caractère 﨑 size=1^諸; si ⁺ est le sous-groupe de B correspondant à face=F9828 n⁺, on a B = M . ⁺ et on prolonge 祥 size=1^諸 en un homomorphisme de B dans C en lui donnant la valeur 1 dans ⁺. Soit alors V size=1^諸 l’espace vectoriel des fonctions f holomorphes dans G et vérifiant l’identité:

pour x 捻 G et b 捻 B. On peut faire opérer linéairement G dans V size=1^諸 en posant:

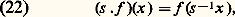pour s , x dans G. On prouve que V size=1^諸 est de dimension finie, que la représentation de G dans V 諸 ainsi définie est irréductible et que sa contragrédiente a pour caractère 﨑 size=1^諸.

On dit qu’une algèbre semi-simple face=F9828 g⁰ sur R est une forme réelle de face=F9828 g si face=F9828 g est isomorphe à la complexifiée:

de face=F9828 g⁰; il est immédiat qu’il revient au même de dire que face=F9828 g⁰ est isomorphe à une sous-algèbre de Lie réelle de face=F9828 g (face=F9828 g étant considérée comme algèbre de Lie réelle de dimension 2n ), formée des éléments invariants d’une conjugaison de face=F9828 g, c’est-à-dire une application semi-linéaire bijective 靖 de face=F9828 g sur elle-même qui préserve le crochet, telle que 靖² = 1. Tout revient donc à déterminer ces conjugaisons, à automorphismes de face=F9828 g près. On montre d’abord que, par un automorphisme de face=F9828 g, on peut ramener l’algèbre face=F9828 u à être stable par 靖. Alors face=F9828 t⁰ = face=F9828 g⁰ 惡 face=F9828 u est la sous-algèbre de face=F9828 u formée des points fixes de la restriction de 靖, et face=F9828 u est somme directe de face=F9828 t⁰ et du sous-espace i face=F9828 p⁰ des X 捻 face=F9828 u tels que 靖(X) = 漣 X. D’autre part, face=F9828 u est l’ensemble des points fixes d’une conjugaison 精 de face=F9828 g, qui permute à 靖; on a face=F9828 g⁰ = face=F9828 t⁰ 簾 face=F9828 p⁰ et face=F9828 p⁰ est l’ensemble des X 捻 face=F9828 g⁰ tels que 精(X) = 漣 X. On voit que la restriction à face=F9828 t⁰ (resp. face=F9828 p⁰) de la forme de Killing de face=F9828 g⁰ est négative (resp. positive) non dégénérée; une telle décomposition face=F9828 g⁰ = face=F9828 t⁰ 簾 face=F9828 p⁰ ayant toutes ces propriétés est appelée décomposition de Cartan de la forme réelle face=F9828 g⁰ de face=F9828 g; elle est déterminée à un automorphisme près de la forme Ad(s ).

Une fois connu un groupe semi-simple compact U, la détermination des formes réelles de son complexifié G revient donc à la détermination des automorphismes involutifs s de U (dont 靖, restreint à face=F9828 u, sera l’automorphisme dérivé s ). Si K est le sous-groupe compact de U formé des x invariants par s , sa composante connexe K⁰ correspond à face=F9828 t⁰; d’autre part, si P est la composante connexe de e dans l’ensemble des x 捻 U tels que s (x ) = x ^-1 (qu’on montre être égale à exp(i face=F9828 p⁰)), on a U = K⁰ . P; le groupe U agit sur P transitivement par: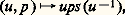

et P est isomorphe à l’espace riemannien symétrique U/K. En outre, l’application (k , p ) 料 kp restreinte à un ouvert partout dense convenable de K⁰ 憐 P, est un difféomorphisme sur un ouvert partout dense de U. Si A désigne un sous-groupe commutatif maximal de P (A est ici un tore), on prouve que tout p 捻 P s’écrit kak ^-1 pour un a 捻 A et k 捻 K⁰, d’où U = K⁰AK⁰ (décomposition de Cartan ).

Par exemple, si U = SO(3, R), groupe des rotations de R³, on peut prendre pour s l’automorphisme t 料 rtr ^-1, où r est une réflexion orthogonale; alors K = O(2, R) et K⁰ = SO(2, R); A est un tore de dimension 1, comme K⁰, et la décomposition K⁰AK⁰ n’est autre que la classique description des rotations de R³ par les trois angles d’Euler .

De la même manière, si G⁰ est la forme réelle (non compacte) correspondant à 靖, c’est-à-dire le sous-groupe connexe de G correspondant à l’algèbre de Lie face=F9828 g⁰, la restriction de 精 à face=F9828 g⁰ est de la forme t , où t est un automorphisme involutif de G⁰; K⁰ est l’ensemble des x 捻 G⁰ invariants par t , et P⁰ = exp(face=F9828 p⁰) la composante connexe de e dans l’ensemble des x 捻 G⁰ tels que t (x ) = x ^-1; on obtient G⁰ = K⁰ . P⁰, et ici l’application (k , p ) 料 kp de K⁰ 憐 P⁰ sur G⁰ est un difféomorphisme. L’espace P est isomorphe à un Rⁿ ; G⁰ y agit transitivement par (x , p ) 料 xpt (x ^-1), et, pour cette action, P⁰ est isomorphe à l’espace riemannien symétrique G⁰/K⁰. On a encore la décomposition de Cartan G⁰ = K⁰A⁰K⁰ (A⁰ sous-groupe commutatif connexe maximal de P⁰), et, en analysant de plus près la représentation adjointe de A dans face=F9828 g⁰, on obtient la décomposition d’Iwasawa G⁰ = K⁰A⁰N décrite dans le chapitre 2.

On voit notamment que les espaces riemanniens symétriques compacts simplement connexes sont en correspondance biunivoque avec les espaces riemanniens symétriques non compacts.

8. Représentations linéaires de dimension infinie

La description des représentations irréductibles d’un groupe semi-simple complexe donnée dans (21) et (22) est un exemple particulier de l’idée fondamentale de représentation linéaire induite , initialement introduite par Frobenius pour les groupes finis, (cf. art. précédent), appliquée aux groupes de Lie.

D’une façon générale, soit G un groupe de Lie, 臨 un sous-groupe fermé de G, F un espace vectoriel complexe de dimension finie, et 﨡 料 L ( 﨡) une représentation linéaire de 臨 dans F. Soit alors V un espace vectoriel (en général de dimension infinie ) de fonctions définies dans G et vérifiant l’identité:

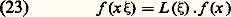pour x 捻 G et 﨡 捻 臨. On fait alors opérer G dans V en posant:

pour s , x dans G.

L’exemple des représentations de dimension finie donné dans (21) et (22) correspond au cas où L est une représentation de dimension 1 et où V est de dimension finie. Le cas le plus étudié en dehors de ce dernier est celui où L est une représentation unitaire (autrement dit, L ( 﨡) laisse invariant un produit scalaire euclidien dans F); si f vérifie (23), on a 瑩f (x 﨡) 瑩 = 瑩f (x ) 瑩 pour la norme euclidienne dans F, et on peut considérer f comme définie dans G/ 臨; on définit alors V comme l’espace de Hilbert des fonctions f sur G/ 臨 telles que:

où 猪 est une mesure sur G 臨 invariante pour l’action de G. Il s’agit de savoir si cette représentation est irréductible, ou de la décomposer en représentations irréductibles; cela pose des problèmes difficiles qui sont encore loin d’être tous résolus. Leur intérêt réside dans le fait qu’ils rattachent à la théorie des groupes de Lie des questions d’analyse ou de physique d’allure toute différente.

En premier lieu, on rencontre ainsi de façon naturelle de nombreuses fonctions spéciales , dont on peut ainsi faire une théorie unifiée et «expliquer» maintes propriétés qui paraissaient fortuites.

Les exemples les plus simples s’obtiennent lorsqu’on prend G = U, groupe compact semi-simple, et 臨 = K⁰ (notations du chap. 7). Alors toutes les représentations de U dans un espace de Hilbert V se décomposent en représentations de dimension finie, le groupe U opérant pour ces représentations dans des sous-espaces de dimension finie V^j de V, dont la somme est directe et partout dense. É. Cartan s’est le premier aperçu que les fonctions constituant les V^j ont des propriétés remarquables. Pour U = SO(3, R), K = SO(2, R), par exemple, on obtient ainsi les fonctions sphériques classiques définies sur U/K = S² (sphère à 2 dimensions) comme restrictions des polynômes harmoniques homogènes dans R³.

On obtient d’autres fonctions spéciales, telles que les fonctions de Bessel ou les fonctions hypergéométriques, en prenant pour G certains groupes de dimension 4.

Si on prend pour G un groupe semi-simple et pour 臨 un sous-groupe discret convenable, on obtient cette fois comme fonctions «spéciales» ce qu’on appelle des fonctions (ou formes) automorphes , qui constituent une vaste généralisation des «fonctions fuchsiennes» de H. Poincaré.

Les fonctions appartenant à V ne sont pas nécessairement continues dans G, mais on peut montrer qu’il y a toujours un sous-espace dense V⁰ de V, stable pour la représentation de G et tel que, pour tout X 捻 face=F9828 g (algèbre de Lie de G), la dérivée pour t = 0 de l’application t 料 exp(t X) . f existe pour tout f 捻 V⁰. Si on note 福(X) . f cette limite, 福(X) devient un opérateur linéaire de l’algèbre de Lie face=F9828 g dans l’espace (de dimension infinie en général) V⁰.

En physique quantique, V est un espace de «fonctions d’ondes», et G est soit le «groupe de Poincaré» (produit semi-direct du groupe de Lorentz SO(3, 1) et du groupe commutatif R⁴), soit (dans la théorie récente des «particules élémentaires») le produit de ce groupe et d’un groupe compact tel que SU(2), SU(3) ou SU(6). Les opérateurs 福(X) sont des opérateurs différentiels du premier ordre; on peut étendre la représentation X 料 福(X) de face=F9828 g à une représentation de l’algèbre enveloppante face=F9828 G (cf. chap. 5); pour k éléments X^j 捻 face=F9828 g,

sera le produit d’opérateurs:

ce sont donc des opérateurs différentiels d’ordre quelconque. Un intérêt particulier s’attache aux opérateurs 福(Z) (dits opérateurs de Casimir ) où Z appartient au centre de face=F9828 G; comme ils commutent avec les 福(X), ils agissent par homothétie dans chaque sous-espace V^j de V où la restriction de la représentation considérée de G est irréductible ; en d’autres termes, les fonctions f 捻 V^j satisfont à des équations aux dérivées partielles 福(Z)f =f . Ainsi, pour G = SO(3, R), le centre de face=F9828 G est engendré par l’unique élément Z = X¹² + X²² + X³², où (X^j ), j = 1, 2, 3 est une base convenable de l’algèbre de Lie face=F9828 so(3, R), et on constate que 福(Z) est le laplacien , ce qui «explique» que l’on obtienne comme éléments des V^j des polynômes harmoniques. En physique quantique, les valeurs propres des opérateurs 福(Z) dans chaque V^j sont mises en correspondance avec les valeurs des grandeurs physiques fondamentales (tels que masse, spin, isospin, etc.) de la «particule élémentaire» associée à la représentation irréductible dans V^j .

9. Généralisations

On constate que les groupes semi-simples complexes sont des groupes linéaires algébriques , c’est-à-dire des sous-groupes G de groupes linéaires GL(n , C), définis par des équations algébriques entre les éléments des matrices de G. On sait d’autre part que les groupes classiques peuvent être aussi définis pour un corps de base K quelconque au lieu du corps C (cf. art. sur les groupes classiques). On est donc conduit à se demander s’il n’existe pas une «théorie de Lie» pour les groupes linéaires sur un corps quelconque K et, comme ici il n’y a plus de notions topologiques, on les remplace par la restriction que les groupes considérés sont algébriques au sens ci-dessus.

On peut alors développer toute une théorie dont les résultats (mais non les méthodes) se calquent sur ceux de la théorie des groupes de Lie (Borel-Chevalley). On définit une notion (algébrique) de «connexion» ^{[cf. GÉOMÉTRIE ALGÉBRIQUE]} et des notions telles que celle de radical, de groupe semi-simple ou de sous-groupe de Borel d’un groupe algébrique exactement comme pour les groupes de Lie. Le résultat le plus remarquable est que, lorsque le corps de base K est algébriquement clos (mais de caractéristique quelconque), les groupes semi-simples sont encore donnés par la classification de Killing-Cartan. Il n’y a plus ici de méthode «infinitésimale» à proprement parler, bien qu’on puisse encore définir une algèbre de Lie face=F9828 g (et même une algèbre associative face=F9828 G) associée à un groupe linéaire algébrique G; mais son utilité est bien moindre que dans la théorie classique. Les raisonnements essentiels sont de nature globale et reposent sur le fait que, pour un sous-groupe de Borel B de G, le quotient G/B est encore muni d’une structure de variété algébrique projective. En outre, on étend encore à ce cas la décomposition de Bruhat (cf. chap. 7), qui joue également un rôle important dans les démonstrations.

Aux groupes linéaires algébriques définis sur le corps des rationnels Q est maintenant rattachée la théorie des groupes arithmétiques : si G est un sous-groupe algébrique de GL(n , Q), on dit qu’un sous-groupe 臨 de G est arithmétique s’il laisse stable un réseau , c’est-à-dire un sous-Z-module de Qⁿ engendré par une base de Qⁿ. Par exemple, SL(n , Z) est un groupe arithmétique dans SL(n , Q). En considérant G et 臨 comme sous-groupes du groupe de Lie G^R (ensemble des matrices de GL(n , R) vérifiant les mêmes équations algébriques que celles qui définissent G) et en utilisant à fond les techniques de la théorie des groupes semi-simples (notamment les décompositions de Bruhat et d’Iwasawa), on retrouve la théorie de la «réduction» des formes quadratiques à coefficients entiers de Hermite-Minkowski et le théorème de finitude de Jordan sur les classes de formes de degré 閭 3 à coefficients entiers, et on les généralise considérablement.

Au lieu de considérer G comme plongé dans G^R, on peut aussi le considérer comme plongé dans G^Qp , où Q^p est le corps des nombres p-adiques (cf. théorie des NOM- BRES – Nombres p -adiques). Comme Q^p est ici muni d’une topologie, la correspondance entre algèbre de Lie et groupe de Lie est presque aussi satisfaisante en théorie p -adique que pour les groupes de Lie réels ou complexes. En utilisant à la fois les plongements de G dans G^R et dans les G^Qp correspondant à tous les nombres premiers p , on arrive aux résultats les plus profonds de Minkowski-Siegel sur les formes quadratiques à coefficients entiers, ici encore largement généralisés et placés dans leur cadre naturel. Il est intéressant de noter que, dans cette théorie, un rôle particulièrement important est tenu par les mesures invariantes sur les groupes p -adiques.

Enfin, la théorie des groupes semi-simples est liée de façon inattendue à celle des groupes finis. Si l’on part d’une base de Weyl-Chevalley (cf. chap. 6) d’une algèbre de Lie semi-simple complexe face=F9828 g, on constate que, pour chaque 見, l’application:

est un isomorphisme du groupe additif C sur un groupe X 見 de matrices qui, en vertu des relations (16), se trouvent avoir des éléments qui sont des polynômes en t à coefficients entiers . Cela permet de définir ces matrices lorsque t appartient à un corps (commutatif ) arbitraire K. En prenant pour 見 toutes les racines de face=F9828 g, on obtient dans GL(n , K) (où n = dim face=F9828 g) un ensemble de matrices qui engendrent un sous-groupe G^K de GL(n , K), appelé groupe de Chevalley sur K associé à face=F9828 g. En particulier si K est un corps fini, le groupe G^K est un groupe fini .

On prouve alors que, si l’on part d’une algèbre de Lie simple complexe face=F9828 g, le groupe de Chevalley correspondant G^K est simple (au sens de la théorie des groupes «abstraits») sauf dans quatre cas correspondant à des corps à deux ou trois éléments et à des algèbres de l’un des types A¹, B² ou G². Ces groupes simples, ont, en outre, des décompositions de Bruhat qui permettent d’étudier de façon détaillée leur structure et qui (pour le cas d’un corps K fini) les distinguent nettement des autres types de groupes simples finis ^{[cf. GROUPES (mathématiques) - Groupes finis]}.

Encyclopédie Universelle. 2012.